偏微分方程式
Partial differential equations
- Elliptic
Laplace equation
- Parabolic
Heat equation
- Hyperbolic
Wave equation
This is amazing visualization.
(How about Laplace equation (elliptic)?)
Parabolic PDEs (e.g. heat) smooth out singularities. Hyperbolic PDEs (e.g. wave) displace singularities. https://t.co/MD3FiWtUid https://t.co/Cw1i8pzqrs https://t.co/v4QMXzodku https://t.co/t0FSBybWtO pic.twitter.com/7Pwx86xWvB
— Gabriel Peyré (@gabrielpeyre) 2018年4月2日
古典力学から量子力学へ
- ニュートン力学の基本法則
Newton's 2nd law
- ラグランジュ力学の基本法則
Lagrange equation
- ハミルトン力学の基本法則
Hamilton equations
ポアソン括弧を用いると
Hamilton equations with poisson bracket
ハミルトン-ヤコビ方程式
Hamilton-Jacobi equation
- 量子力学の基本法則
Schrödinger equation (time-independent)
ポアソン括弧
ニュートン力学から、ラグランジュ力学になって、ハミルトン力学になる。
ラグランジュ力学から、ハミルトン力学になるときの「ルジャンドル変換」については、こちらのサイト forXiv に書かれていた。
特にこの図 inverse graph が分かりやすい。
しかし「ポアソン括弧」が分からなかった。Wikipedia には以下のように定義すると書かれている。
少し調べると、どうやらこちらのサイト StackExchange に書かれていた。
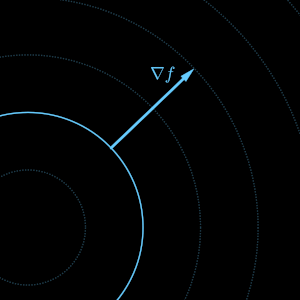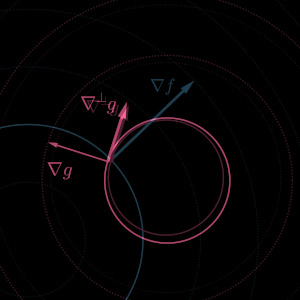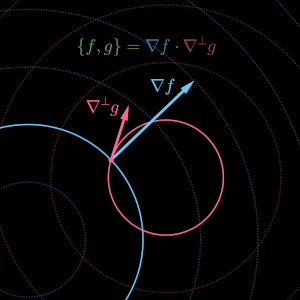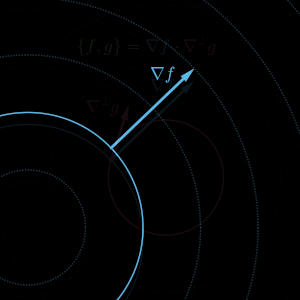
the dot product in phase space of the 'ordinary' gradient of
and the symplectic gradient of
.
ということらしい。式で表すとたぶん以下のようになる。
このことを式で表そうとしたときに、Wikipedia で Skew gradient なるものを見つけた。
ここで という記号が使われていて便利そうだったので使ってみた。
たとえば は、いたるところで、
と直交するベクトル場のことだ。




k-form と tensor
- k-form と tensor ってなんか似ているのかな、と思ったら tensor の特殊なもの(交代性があるもの)が k-form みたいだった。なので tensor で交代性のないもの、たぶん対称なものもあるみたいだった。Symmetric tensor と Antisymmetric tensor。
memo
Stokes’ theorem
Change over Area = Amount over Boundary
- Derivative of Amount = Change
- Derivative of Area = Boundary
k-vector
- Scalar
- Vector = Ordered scalars
- k-vector = Ordered vectors
微分形式
Meaning
| primal | dual |
|---|---|
| vector | covector |
| k-vector | k-covector |
| vector field | covector field |
| k-vector field | k-covector field |
Standard
| primal | dual |
|---|---|
| vector | 1-form |
| k-vector | k-form |
| vector field | (differential) 1-form |
| (k-)vector field | (differential) k-form |
記録をとること
5月10日(木)
寝不足なのかなんなのか、すごく眠くて少し寝てしまった。気圧のせいだろうか。この頃、気温の変化が激しくて体調にも影響があるみたい。睡眠はきちんと取っているのだけれど。
数学の説明動画はあきらめつつある。プログラムで描けばきれいなのではと一時は思ったけれど、微調整が大変そうなのであきらめた。それなら動きはカクカクだけど、既存のソフトを使うほうが速い。
こうやって書いてみないと自分がそもそも何をやろうとしていたのか忘れる。何をやろうとしていたんだっけ。多分このままじゃいけないと思って何でもいいから何か新しいことを始めようとしたんだった。
読書のほうはどんな感じか。「Love and Math」は13章あたりまで読んだ(朗読を聞きながら)。「数学ガール」の最新刊はさささっと早めのペースで読んだ。何回か読み直したい。「Burn Math Class」はもう一度、序文や序序文を読みなおした。やっぱり数学の Logical な面でなく、Plausible な面に注目しているんだなということを確認した。内容は少し冗長な感じで今の自分には合わなそうで、あまり読めていない。
仕事、変えたほうがいいだろうか。毎年こんなことを言っている。ただ最近は、ひとつの仕事を「やる・やらない」ではなく、ふたつくらいの仕事の「バランスを調節していく」ほうがいいのでは、という風に考えたりしている。「やる・やらない」だとかなり勇気のいる決断が必要になる。大きな決断というか。そうではなくて、ひとつの仕事を続けつつ、ほかにもできそうなことを探すのが理想な気がする。そんな風に考えるほうが、弱気な自分に対してもプレッシャーが小さい。
今のところ、そのもうひとつがなかなかつかめずにいる。でも何でもいいからやってみよう。「数学の動画をつくる」というアイデアは少しきびしそうだ、というのが分かっただけでもよかったではないか。きびしそうであれば、次のアイデアを探していこう。何かしらはあるはずだ。
気になっている本「Visual Complex Analysis(複素解析)」「Visual Group Theory(群論)」「Love and Math(数学一般)」「数学ガール(数学一般)」「Mathematical Method for Classical Mechanics(物理数学)」
いろいろチャレンジしてみるにしても記録は取っておかないと、自分でも何をしているか分からなくなる。今の状態がそれに近い。できるだけこまめに記録をとろう。
動画と読書
数学を説明するブログを作ろうと思い立つ。読んだり見たりするだけでは、ある程度以上は身につかないだろうと思ったからだ。あとSNSで読んだファインマンの言葉の影響もある。できるだけ視覚中心にしたかったので、まずは絵から作りはじめる。とりあえず静止画。次に簡単なGIF動画。思った以上に時間がかかる。特に動画は大変だ。これは重労働だ・・・と思い、動画はほとんど断念する。では静止画かというと静止画だと今度はイメージが伝わりにくくなるように思う。なかなか難しいのだな。でも動画を作るのがどれだけ大変か、静止画はイメージが伝えにくい、ということが分かっただけでも勉強になった。
やっぱり気になって自分の好きな動画作成者のページに行ってみる。動画を作るために書いたコードがすべて公開されているので、内容は分からないけれど量やかかった期間などをみる。「この量・・・この時間・・・、もしかしてものすごいエネルギーが必要なんじゃないか・・・」と半ば自分を納得させる。さらに概要の説明で、以下のような文があった。
For 9/10 math animation needs, you'd probably be better off using a more well-maintained tool, like matplotlib, mathematica or even going a non-programatic route with something like After Effects.
「そうか・・・ふつうの人は既製品で十分なのか・・・」とまた自分を納得させる。
- Amazonで「Love and Math」が割引されていたのでポチってしまった。読めるかなと心配していたけれど、夢中になって読んでしまった(まだ途中)。その中でこんな文章が心に残っている。
Don’t get me wrong: reading this book won’t by itself make you a mathematician. Nor am I advocating that everyone should become a mathematician. Think about it this way: learning a small number of chords will enable you to play quite a few songs on a guitar. It won’t make you the world’s best guitar player, but it will enrich your life. In this book I will show you the chords of modern math, which have been hidden from you. And I promise that this will enrich your life.
長いけど、要は「ちょっとかじっただけで数学者になれる訳じゃないけど、人生を豊かにはしてくれる」という感じだと思う。しかもギターを比喩にしている。かっこいい・・・。でも言っていることも納得できるし、学んでいくことに対して前向きな気持ちになれる言葉だ。
できたらここまで読んできたので、各章ごとに取り上げられていた話題を簡単にまとめておきたい。それは後日やろうと思う。この前書きだけでなく、もちろん内容もおもしろい。
多様体、接ベクトル空間、ベクトル場
難しそうなワード
なんか難しそうなワードが並んでいるけれど、考え方は基本と同じっぽい。
低次元のときでいうと、多様体は曲線とか曲面だし、接ベクトル空間は接線とか接平面だし、ベクトル場はベクトル場だ。
なんでこんなことを考えるの、という疑問に対しては、低次元のときと同じ答えになるのじゃないだろうか。
たとえば、多様体は「関数や写像を図形で表すこと」だし、接ベクトル空間は「多様体を1次近似すること」だ。
低次元でいうと、曲線や曲面は「関数を図形(グラフ)で表すこと」だし、接線や接平面は「曲線や曲面を1次近似すること」だ。
なんで高次元にするか
なんで高次元にするかというと、自由度が上がるからだ。
曲線や曲面だと変数は2,3個までしか使えない。
でも別に拡張してしてしまえば、もっと自由度が上がる。
たとえば、入力でも出力でもすごいたくさんの変数をもつ写像があるとする。
それは多様体から多様体への写像になる。
そのまま考えられればいいけれど、あまりに複雑すぎる。
そこで接ベクトル空間が出てくる。
その複雑な写像を1次近似することで、特徴をつかもうとするのだ。
という風に考えてみたのだがどうなのだろう。
具体的な応用例
具体的な応用例があげられるとよいのかもしれない。
たとえば100個の変数があって、写像を通すと50個の変数が動く。
そういう写像があったとして、どんな写像かをざっくり知りたい。
そんなときはその写像の接ベクトル空間を考える。
すると写像の特徴がある程度分かる。
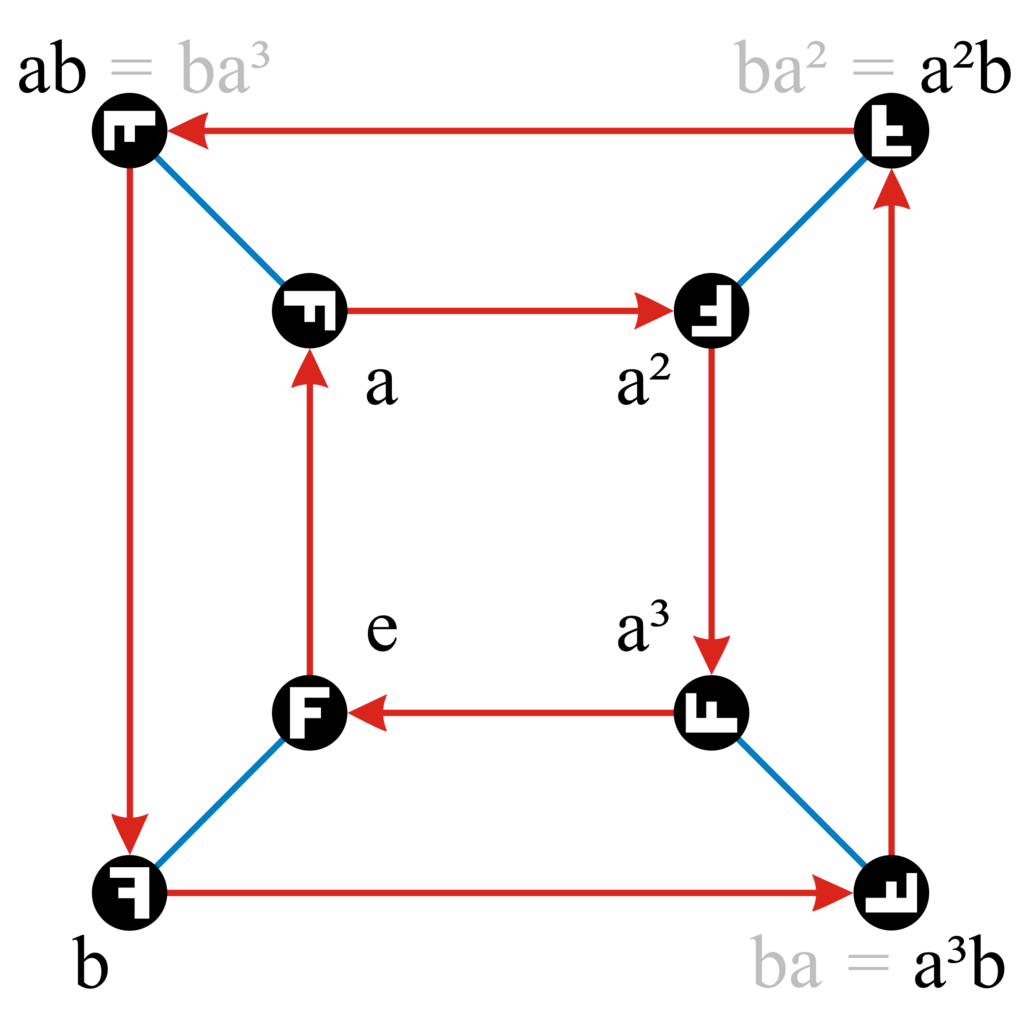
ケイリーグラフ
ケイリーグラフ:群の中である特定の置換に注目して描いたグラフ。元と元の間のすべての関係を表しているわけではない。
3次の対称群と交代群
(回転と反転)


4次の対称群と交代群
(回転と反転?)


5次の交代群と4次の2面体群